Randomised Controlled Trials in peacetime
- Matteo Quartagno

- Aug 2, 2020
- 8 min read
Updated: Aug 3, 2020
Why are they considered the standard?

In a hospital, two leading doctors cannot agree on the value of a specific treatment. They call a statistician to discuss.
Doctor A: I really believe that Quartax cures all patients with Z. We should give it to all Z patients, NOW!
Statistician: how can you be sure? What are you basing your beliefs on?
Doctor A: on my experience! I gave it to three patients and they all healed! Statistician: but how can you know they would have not got better anyway? Let me show you this video:
Has this guy stopped the train?
Doctor A: That's not the case here, I am sure that Quartax works!
Statistician: as are between 70% and 95% of drug producers whose ideas in the end are not backed by Randomised Controlled Trials (RCTs).
Doctor A: you keep talking about these RCTs...
Statistician: Yes, because Randomised Controlled Trials are the standard in clinical research to investigate effectiveness of treatments.
Doctor A: Why is that the case?
Statistician: To keep it simple, they are the only way to guarantee that the assignment of one treatment over another is not driven by specific factors, but completely random, and therefore differences in the outcomes cannot but be due to the treatment itself.
Doctor B: does this mean we will compare two completely identical groups of people, one getting Quartax and one standard of care?
Statistician: more or less, but not precisely. Loosely speaking, this is just true on average (statisticians would say in distribution); one will never achieve perfect balance between groups on any single possible variable [as I explained here]. The advantage of RCTs, though, is that they reduce confounding to error, and can then be designed with the goal to reduce that error as much as possible. Running multiple trials will then make repetition of the same errors less and less likely.
Doctor A: wait, wait, I am losing you! What does this all mean? Give me a practical example!
Statistician: In the last months everyone will have read articles or blog posts with claims such as "In the hospital X, where people use Y, Covid deaths have been way less than in the rest of the world!", or "In country X, where people are more Y than the rest of the world, things have gone much better!". As a rule of thumb: never trust any of these claims. EVER. There are several reasons why things could have gone differently in hospital or country X compared to the rest of the world, and this might have nothing to do with Y. Such a simple analysis is both subject to a high probability of random error and to systematic confounding.
Doctor A: Again, what does this mean exactly?
Statistician: Ok, let me try and explain. First, there can be random error: let's take countries starting with a consonant in my surname, so Q,R,T,G or N, and compare them with countries starting with B or S (which make up an acronym chosen not at random) in terms of Covid deaths/million people (taking these numbers from Worldometer). What is the average number of deaths per million people in the two groups? QRTGN= 37 deaths/million BS = 125 deaths/million
So there is on average a difference of 88 between the two groups. A huge difference! But you are not to be fooled, you want a confidence interval rather than just a single number, right? The 95% confidence interval is [12, 164]. It excludes the 0, so all good right? We can even add a nice p-value of 0.024, telling us that under the null hypothesis that there is no difference between countries starting with QRTGN or BS in terms of Covid deaths, we only had a 2.4% probability of observing such extreme results, or more extreme. Therefore having B or S as initial did make a difference! I think I can safely assume you will find this to be a stupid conclusion. This is clearly a spurious result. With other characteristics, it would be much harder to convince a reader that the result is spurious. Say we did the same with Vitamin D levels, or flu vaccination for example. By doing a controlled experiment, we do not exclude the probability that we might be unlucky and get a spurious result, but we pre-register the analysis we want to do, limiting the chance to cherry-pick the desired result, and we limit the probability to get such a spurious result by chance to a small value. And possibly we repeat multiple independent studies, to make the probability so small to be negligible. If instead we somehow take some numbers and compare them, we have no way of controlling errors. For example, in this case I clearly just made this example up after noticing nations starting with letter B and S did particularly bad. So everyone can make their own example, trying to fit their own agenda.
Doctor B: but you do not need a randomised trial, you might just pre-register any analysis before it is performed.
Statistician: Sure thing, though perhaps it is at times difficult to make sure the analysis is really pre-registered, particularly when it is done with retrospective data. But there is one thing for which randomisation is fantastic: confounding.
Sometimes, results might not be spurious, but due to confounding factors. Roughly speaking, this means there actually is a difference between two groups, and not just in our data by chance, but it is not due to the factor we are investigating, but to something else that is associated.
Let's do a similar example to the one above, but comparing countries in terms of average rice consumption. Let's select countries that have been discussed extensively in terms of their handling of the crisis: China, Italy, Sweden, UK, France, Spain, Brazil, Hong Kong, Vietnam and South Korea. Let's try to estimate the relationship between average annual rice consumption per capita and number of Covid deaths per million inhabitants (on the log scale).
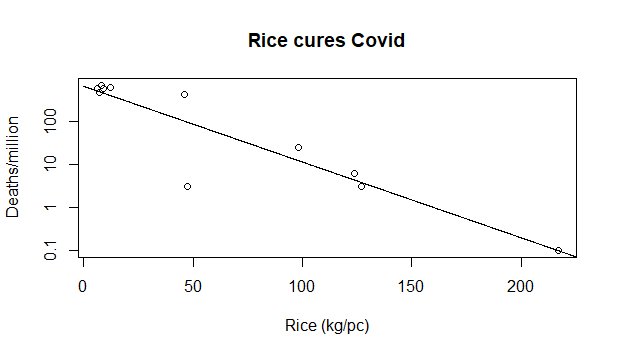
Looks like a clear relationship! The more people eat rice, the less they die of Covid! But again, you're not easily deceived, you want to see an estimate of uncertainty, or at least the p-value from a test telling you whether this line is not likely to be different from a horizontal one just by chance. The p-value is 7.24e-05, which is statistics-ese for "No way this happened by chance".
Note this time I did not have to cherry pick the nations to include. I honestly just selected some of the most discussed nations, suspecting I would have seen this relationship in the data. Of course, it might still be that this result is completely due to chance as in the previous example, but I believe in this case the explanation is different: Asian countries have fared far better than European and American ones in this epidemics. We don't know 100% why, but it might have to do with a lot of factors that made them more prepared, like having had recent epidemics, having in some cases strong centralised state, or in some others good hygiene. It would have to be established precisely. At the same time, Asian countries eat way more rice on average than Western ones. So, being an Asian country affects both the amount of rice eaten on average and the number of Covid deaths. We say that it is a confounder of the association between deaths and rice consumption and, if not spotted, can lead to quickly conclude that eating rice leads to less deaths. It might be (I really don't think so, but in theory...) but it is much more likely that a combination of the other factors I listed above is instead responsible for the lower death rates.
Doctor B: I get it. So, if we just observe a difference between two groups, it is not enough to conclude anything, because it might be due to random error or confounding. Are these the only possible problems? And why you think that RCTs fix them?
Statistician: Unfortunately, there are other possible problems in interpreting such comparisons, for example ecological bias. But I don't have time now, we can discuss those another time. You asked me how RCTs address random error and confounding? Trials limit to a desired level the probability of random error. Common choices are to limit to 2.5% the probability to claim something to be superior to standard of care if it's not, and to 10% the probability of not declaring it superior if it is by a certain amount. By running different trials (or simply a huge one, if possible) those can be limited even more.
With regards to confounding, instead, we use randomisation to guarantee that any difference is on average due to the treatment only. And if we spot any difference in a known risk factor between the two groups, for example, if the age distribution ends up different between people who take Quartax and people under standard of care, we can take that into account in the analysis.
Doctor A: Yes, bla bla, RCTs are theoretically great, but you can't do one for everything! See, eg, the effect of smoking!
Statistician: True, in the second example we could not randomise entire countries to eat or not to eat rice. But nobody ever said that (EVER). The point is simple: if you can randomise, do it. If you cannot, do the best you can. Note "the best you can" is far from "plot X versus Y" in general. Your sentence sounds a bit like: "Sure, stealing is wrong, but if you are without any money, you will have to do it to eat!".
Doctor A: bah, regardless, RCTs are extremely difficult to perform, require huge resources and time...
Statistician: Sure, but good research is costly and difficult, no matter what. And bad research is often costly as well. Only difference is that, although perhaps less difficult, bad research keeps costing when it's over.
In terms of time, it really depends on the application. Pandemics have proven to be a situation where recruiting patients can be done extremely quickly (RECOVERY...) compared to standard, for example.
I mean, you are basically saying: "A Mercedes is faster than a FIAT Panda, but it costs too much, so I am going to run that Formula 1 GP with my Panda."
Doctor A: Even if that was the case, RCTs are too specific, they only answer a very limited question for a very limited population
Statistician: Yes. But that is also one of their advantages. It means that you have to very carefully think about the hypothesis you want to test, the people this should apply to, the doses you should give, etc etc. And that by the end of the trial you will have a very specific answer to a very specific question. Rather than a very noisy answer to a very general question. Doctor A: You have an answer to everything, I am sure you would do RCTs to test parachutes!
Statistician: well, I do hope that those who manufacture parachutes do something more than hoping they work and saying "we can't let people jump off the plane without anything" before they start selling them!
And besides, with most parachutes vs no parachutes we are talking >99.9% vs <0.1% survival probability, which is quite different from pretty much all clinical research, where a difference between 80% and 75% is often considered miraculous!
Doctor A: but that's the case here! Quartax truly is miracoulous, all of my patients healed!
Statistician: if that is truly the case (I strongly doubt that, but nevermind), we can have interim analyses and if at some point the advantage appears to be clear, we can stop the trial and start giving Quartax to everyone.
Doctor A: OK... let's do this trial... But this time, design it better! Last time, when I proposed Mattex, the trial failed only because it was underpowered! The treatment effect direction was favourable!
Statistician: so you were able to understand it works from observation on 3 patients, and you thought a 1000 people trial was underpowered? Interesting! Seems a bit like you were saying "the shot looked like it was heading towards the goal and if I'd hit it a bit harder it would have curled in! [sentence stolen from Tim Morris]" Reminds me of some claims I read about Covid treatments...
Doctor A: so wait, I am happy to allow you to be so overly conservative in peacetime... But now you are going to tell me RCTs should be the standard even during a pandemics! That's crazy!
Statistician: yes I am! We don't have time for this today, but we can talk about it tomorrow...




Comments