How to interpret COVID-19 research news
- Matteo Quartagno

- Apr 25, 2020
- 22 min read
Updated: Apr 26, 2020
Data reliability, test performance, causality and clinical trials
There are those sorts of events that either are so intrinsically important, or capture so much our attention that we end up asking the same question over and over again: where were you when that happened? How many times have you (been) asked "what were you doing on September, 11th"? Among Italians, the most common question of this kind is: "what did you do when Italy won the World Cup in 2006"? (I know, everybody has their own priorities).
I started this blog a couple of months ago, when the world (at least the Western one) was still apparently quiet, but now that things have changed I wonder whether in few years time I will ask myself "what were you talking about during the Covid pandemics?". It would definitely seem weird to come back to this space not finding any reference to what has been described as the most shocking global event after the end of WWII. Up until now I had decided not to talk about it here for various reasons: first, because I believe there are people who know far more about this virus than I do. I really do not want to become yet another last minute infectious disease epidemiology expert, based on a quick Google search. Yet, working in medical research, I am quite familiar with many of the concepts discussed these days, and so I thought I could write a post trying to help people that are not familiar with either statistics, or medical research, or both, to make sense out of the tons of info we are bombarded with every day. This post is divided in 4 parts, broadly discussing data reliability, test accuracy, causal interpretations and drug development. I tried to focus on things that I know, and stress whenever I was talking about something I am not an expert in. Of course, if you disagreed on something, do let me know!
1) Data are not a perfect representation of reality
Don't tell Trump this, but whenever developing new statistical methods, it is common to start from fake data. These are data that are simulated by us, so we have perfect knowledge of their generating mechanism and we can judge whether our new method performs as expected or not. Generally, if the method works with fake data, the next step is to apply it to real data. Junior researchers often don't understand why more senior ones put so much emphasis on applications on real data as a step in method development. At least I didn't. In the end, if a method works on data generated by me, why shouldn't it work on data generated by the world? Numbers are numbers. Why are real data supposed to be better than fake data? The answer is that they are not: they are far worse.
There is pretty much no study or experiment where the data collected can be considered to be perfect. There are all sorts of sources of errors and imprecisions. Indeed, much of early statistics was developed exactly to deal with imperfect measurements. In particular, the development of the least squares method, one of the most simple statistical methods to fit a line across data, was driven by the need to account for measurement error in observation of celestial bodies. This was across the 18th and the 19th century. More than 200 years later, we still need to rely on approximate measurements when collecting all sorts of data.
There are, roughly, two possible types of error: random and systematic. Random errors are, broadly speaking, easier to deal with. If the variable affected by random error is the outcome of our analysis, i.e. if it is the main variable of interest, then it's often enough to treat it as a random variable as explained in this previous post. More generally, though, things can get trickier.
With Covid data, what is possibly more intersting, though, is the second type of error, the systematic one. As by now we probably all know, it is virtually impossible for any nation to keep track of all Covid infections. Some do better (South Korea), some worse (pretty much all the West), but the infections count is likely to be a vast underestimation of the true number for all nations. One possibility to try and adjust for this sort of errors is to use other available (and correlated) data, considered more reliable, to correct our estimates. Take for example Covid infection and death counts. Death toll is surely a more reliable number, as there is no such a thing as a mild death. Let's put aside for a moment the probability that even data on deaths might be doctored. How can we use data on deaths to get a better estimate of data on infections? What we need is a good estimate of how the two are linked. The number we need is the Infection Fatality Rate (IFR), the proportion of infected people that eventually die in a population. The last 3 words are important. This number can vary between different populations. So, we also need a summary of population characteristics: how many old people are there in Italy compared to China? And in Vatican City?
Combining data on deaths, IFR and population characteristics, we can get a possibly better estimate of the total number of infections. However, the problem is that, of course, there is no guarantee that the corrected estimates are actually going to be better than the crude ones. This depends on the quality of the more reliable data we use. Data on population characteristics are generally super reliable, but what about the other two?
To have a good estimate of IFR, we need to have good data on infections, at least in a limited area. So the problem is somewhat circular. Furthermore, IFR might not be stable and it generally increases when health systems reach their limit. There is also strong suspicion, if not simply evidence, that even the number of deaths might be a huge undercount. Data from the Italian town of Nembro, from Madrid or more recently from the Office of National Statistics have shown that the true numbers might be much larger. This is mainly because a lot of people, particularly older people living in care homes, often die without having been tested or brought to the hospital.
What stems from all of this is quite simple: no number should be taken at face value. They should be interpreted only by people with some insights into data collection practice. I am not talking just about differences across nations. Even comparing the same number for the same nation at different time points might not be that simple if, for example, data collection practice changed over time. Think for example of the number of weekly tests in several nations, which has steadily increased in the last couple of months. As I started this post, remember: this problem is by no means specific of Covid data. Quite the opposite, given the huge global attention, we are collecting way better "live data" than usual. Ever known anybody tested for the flu? So why do we trust the flu numbers? How do we get them in the first place?
There are strategies to estimate the true number of deaths and infections of an outbreak a posteriori, once it is over. One way is estimating excess deaths, that is how many more people died overall compared to how many we would have expected without the disease. For example, compared to the average of the same period over the last 5 years. Of course this can be tricky if there are interactions, for example if more people die as a secondary effect of the pandemics even without being infected (for example people having heart attacks who prefer not to go to A&E...) or if people staying home actually decrease the number of deaths from other causes (for example because people are not driving any more). One way to estimate the number of infections a posteriori is instead to randomly sample from the population of interest to test for the presence of antibodies against the infection. The method is broadly the same used to do opinion polls for general elections. Barely, people are just asked a single question, and they respond with their blood rather than their words. Still, the answer might not be perfect. What if antibodies do not last much, and have already vanished by the time a person gets tested? What if the test gives a wrong answer. This leads us to my second point...
2) Immunity certificate are appealing, but difficult to realise.
The UK has been the first country to propose them, almost a month ago: immunity certificates could give people the opportunity to get back to normal life, once a test will certify they already had the infection. There are still possible organisational and psychological issues with this: wouldn't this encourage people to try to get infected to go back to work? Wouldn't it discriminate against people who were not infected? There are also clinical uncertainties: are we sure that somebody who's found to have antibodies is not still infected? And for how long will this immunity last?

I promised, though, not to talk about things I don't really know, so my considerations are rather more technical. The system to release these certificates, would probably be based on home self-test kits, not too dissimilar in concept from simple pregnancy tests. No test is perfect, though, and particularly those taken at home, with no specialist involved. You may test positive even though you were never infected (False Positive) or you may test negative even though you had the infection (False Negative). There are two numbers that are used to quantify the goodness of a test: sensitivity and specificity. The first tells us how much the test is sensitive, hence what's the probability that if you ever had the infection, it will find the antibodies. The second tells us how much the test is specific, so what's the probability that, if you did not have the disease, you will test negative. For the first home kits developed, these numbers seem to be at around 95%. Fantastic, you might think, let's produce millions of them and start back the economy! Well, not quite. It all depends on the proportion of population infected. Let's do some simple math: - Let's assume we live in Luckyland, a country with exactly 1 000 000 inhabitants, 1% of whom only contracted the virus at some point. Therefore there are 10 000 immune citizens and 990 000 non-immune citizens. - Let's assume we test all the citizens with our kit, with 95% specificity and sensitivity. - Out of the 10 000 immune citizens, 95% will test positive, because sensitivity is as high as 95%. Hence, 9 500 immune citizens will be able to rightly leave quarantine.
- Out of the 990 000 non-immune citizens, though, about 5% will test positive by mistake, because specificity is only 95%. So, 49 500 people will be told they had the infection even if they didn't, and will go back to work/restaurants/life as usual, despite being still susceptible to the virus. - Overall, after testing the whole population, 9 500 + 49 500 = 59 000 people will go back to work, out of whom 49 500 / 59 000 = 84% will not really be immune. That's more than 4 out of 5 people being given the all-clear by mistake!
The numbers are sobering, and are due to the fact that, given the low number of patients infected, the false positives outweight the true positives. In other countries, with higher proportions of patients infected, conclusions might differ:
- If we lived in Mediumland, again inhabited by exactly 1 000 000 people, out of whom 10% were infected, 95% of the 100 000 immune would test positive, together with 5% of the 900 000 non-immune. That's 95 000 true positive, vs 45 000 false positives. Still nearly 1 in 3 people resulting immune, will not really be so. - If we lived in Doomedland, where 50% of the 1 000 000 inhabitants were infected, things would start to make more sense: 95% of the immunes would be given the all-clear, vs 5% of the non-immunes. Only 1 in 20 people would go back to life as normal by mistake, exactly as the 95% specificity would have suggested.
The implication is that, at an individual level, if you test positive you are likely to actually have had the disease only if you lived in a high prevalence area. In areas not much affected by the virus, the test would be pretty much useless. But I hear you say: how come the probability that I am infected depend on other people? Didn't you say that this specificity thing meant that I had only 5% probability of being found positive by mistake? The difference is subtle. Specificity is the probability of testing negative given you were negative. But you do not know whether you were negative or not. What you are more interested in at an individual level is the inverse probability, that of being positive if you actually tested positive.
This is probably best explained as an example of how a particular type of statistics works: Bayesian statistics. It is sometimes called inverse probability statistics, precisely for the reason I just described. I will go into the details of this in another post soon, but roughly the idea is that we start with a prior probability, we complement it with data and we obtain a posterior probability:
Prior = 1% of the population is infected. If we ignored things like having had symptoms or similar, our prior probability of having been infected would be 1%. We are a random person from the population of Luckyland. Data = Our test is positive. We can complement our 1% probability of being infected with data coming from this test. Posterior = Given our prior probability of 1%, and the result of our test being positive, our probability of having been infected is now around 16% (100-84%). Of course, it could be possible to improve these numbers repeating the test multiple times. For example, if we tested everybody twice, and we assumed that the results of the two tests were independent, the probability of obtaining two consecutive false positive tests would only be 5% of 5%, i.e. 0.25%. If we required both tests to come out as positive to give somebody an immunity certificate, the probability that the individual was truly positive if both tests came out positive would now be 78% instead of 16%. But remember, this requires the two tests to be independent. If the reason for the false positive was something systematic, then 2 consecutive false positives would be highly likely, and the proportion of non-immune people testing positive much higher. The last point to consider is that all of this is valid because we are interested in knowing whether someone was infected at the individual level. If we were interested in the prevalence of the disease in the population instead, and not in who were the specific people with the disease, then knowing specificity, sensitivity and number of people testing positives would be enough to have a good estimate of the population immunity using simple correction rules. This would only require solving a simple system of equations. Here, TP (True Positive) is the unknown number of people truly infected, and TN (True Negative) the unknown number of people never infected:
Equation 1 : TP * sensitivity + TN * (1 - specificity ) = n of people testing positive TP * 0.95 + TN * 0.05 = 59 000 (in Luckyland) Equation 2 : TP * (1 - sensitivity) + TN * specificity = n of people testing negative
TP * 0.05 + TN * 0.95 = 941 000
If you did study how to solve systems of equations in secondary school, you will know how to easily solve this system of two equations in two variables, to get these results: TP = 10 000 and TN = 990 000. TA-DA! So, after testing the whole population, the burocrats in Luckyland will know that only 1% of the population actually had the infection, but they could not know which of them had it individually, out of the more than 5% testing positives. Immunity certificates would be dangerous. On the contrary, in Doomedland they would have a much better idea of who catched the virus, but 50% of the population would have had it already. So herd immunity would have possibly almost kicked in. Immunity certificate would still be superfluous.
3) Causality should guide research The mantra is so pervasive that even if you never studied statistics in your life you likely came across it at least once: correlation does not imply causation. History is full of examples of studies showing correlations that clearly have no causality implications. Some are due to confounding factors: brushing your teeth every day is associated with living longer on average, (most likely) not because it causes an actual improvement in survival, but because people who brush their teeth twice a day are more likely to live healthier lives, and hence live longer on average. Other times, the correlations are just ramdomly spurious: there is even a website listing tenths of examples, things like the divorce rate in Maine being 99% correlated with margarine consumption, or the number of movies Nicolas Cage appeared in yearly being 70% correlated with the number of people drowning in pools.
Is it actually possible to distinguish between correlation and causation? For years the answer statisticians used to give has been mainly "no". The only tool that was recognised to be useful at detecting causal relationships were clinical trials. A clinical trial is designed so that similar people are given different treatments at random, so that, on average, they only differ because of the treatment they receive. Hence, if some effect is detected, it is likely caused by that treatment. In a sense, this tackles on average the first type of correlation-notcausation examples, those caused by confounding factors, but not the second, those completely spurious. This is because patients will be similar on average, but there is still going to be some variation. Randomisation reduces imbalance to error, but does not eliminate it. Trials are usually designed, though, in such a way that errors are minimised as much as desired, under certain assumptions. If several trials are (well) designed on the same treatment, only few of them will give the "wrong" results by chance.
Trials can be very complicated to design, conduct and analyse. For this reason, a lot of research is still observational in nature. This means it does not involve designing a thoughtful experiment, but only looking at data observed in real life. If this is done naively, it is the perfect way to look at correlations that do not necessarily translate into causation. However, there are actually tons of methods to do causally-valid observational analyses. These have been developed at an incresingly fast pace over the past 40 years. How do they work?
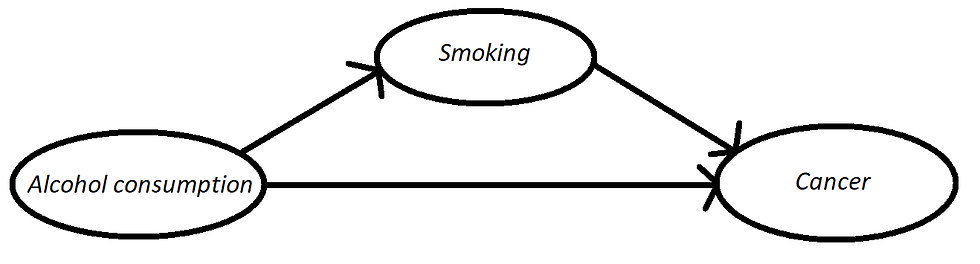
The basic idea is: you write down the mechanism that you believe to be in action given your experience in the field. Usually this is done by drawing so called Direct Acyclic Graphs (DAGs), simple graphs depicting causal relationships. Then, there are methods both to (i) know from the graph if you can estimate a certain causal effect and, if you can, to (ii) actually estimate it, modifying your simple "correlation analyses". Of course, there is still no guarantee that your causal model will be correct. Results depend on all your assumptions. Starting from the validity of the causal graph drawn. Why am I talking about all of this? Well, one of the things that strikes me the most about these days, is the amount of articles/blog posts showing "surprising correlations" and claiming with no doubt to understand the causal mechanism behind them. This was maybe OK 40 years ago, but not today. If we believe a certain mechanism is in action, we should do a causal inference analysis, before claiming so with any degree of certainty. I have read quite a lot of papers on Covid and, at the moment, I am still to read one that uses causal inference models extensively.
If you asked me some time ago, I would have told you that papers on correlations alone are fine: they are a necessary first step, their results can be used to conjecture a causal model, that can then be tested at a second stage. However, this pandemics has to me clearly indicated the danger of correlation-based analysis. Often, people stop researching as soon as they see the results of the correlation analyses, and keep claiming they know the causal mechanism before going on to the second stage, designing a study and/or analysing the data with this causal mechanism in mind.
Take for example this article, which made the headlines in The Guardian. The authors claim that:
"The results indicate that long-term exposure to [...] pollutant may be one of the most important contributors to fatality caused by the Covid-19 virus in these regions and maybe across the whole world".
The article goes on to say:
"The analysis is only able to show a strong correlation, not a causal link".
Fantastic, but then why to write the previous paragraph? An article about science should be just about science, using the verb may does not allow us to write an opinion piece as if it was a scientific one.
The huge problem is that most readers (or at least, most non-climate-change-denier readers) will be convinced that science has proved this relationship to be causal after reading this article. The second sentence will simply be skipped. My view is that correlation studies are only OK for experts to check whether it is worth examining a certain causal mechanism. Why not to wait before publishing the news in generalist newspapers until a more causally-sound analysis has been performed?
4) How to find a treatment or a vaccine
I left this as the last topic, but it is possibly the most important, the one is worsely explained by media and known in the general population. Development of drugs, either vaccines or treatments, is a very long and hard process. It has to be so. For a simple reason: you can't play games with people's lives. You need to make sure you have done the most accurate and honest research possible to be sufficiently confident that what you developed is both safe and effective.
At the risk of oversimplifying the process, there are roughly 4 phases in the development of a new drug:
Phase "0": computer models, in vitro experiments and animal experiments to shortlist the most promising candidates. Let's suppose after this phase, the most promising treatments are pizza and dead rats.
Phase 1: We need to start giving treatment to healthy volunteers, to make sure it is not unsafe. Initially, we have no interest at all in the effectiveness against the disease. We just want to make sure it is not dangerous. Of course,we already know that pizza is not dangerous, but we possibly cannot say the same about dead rats. So we need a phase-1 study to investigate their safety.
Phase 2: We now know that both pizza (from overwhelming evidence) and rats (after phase 1 trials) are safe (well, bear with me...). The next thing is to start exploring whether they are effective, starting to experiment on a limited number of patients affected by the disease. This is a good opportunity also to optimise dose and duration of treatment. How many pizzas a day? And for how many days? It is also important to keep checking whether they are also safe on patients, rather than healthy volunteers. You'll never be 100% sure that dead rats are safe.
Phase 3: If after phase 2 both treatments were still found to be safe, and if there was a suggestion they were effective against the disease as well, it would finally be time to run the final, large, study, to evaluate their actual effectiveness against the disease. These final studies would (almost) definitely answer the question: are pizza or rats better than current standard-of-care?
In standard medical research, these phases usually last for years and years. It can be 10 years or more between phase 0 and the moment the drug is licensed. Of course in such a situation of emergency, things could be sped up, but at some costs. The long times are not generally needed just for fun, but for good reasons. Speeding up times too much could lead to several problems. We might miss medium-long term side effects. We might evaluate outcomes in a too short time frame. We might simply prepare a bad study design and/or do a bad analysis: as per an Italian proverb, the hasty cat delivers blind kittens. As with all studies, rushed studies can be badly designed in good faith. But, in these situations, emergency is sometimes used to justify a terrible study implemented simply to maximise the chance to find a positive result. There are several examples from recent days. The most famous is the Raoult hydroxychloroquine's study (HCQ).
Didier Raoult is a French "contrarian" (aka attention-seeker) doctor, working in Marseille, who started with his group a study to investigate the use of HCQ to treat early Covid infection. What is the best way to investigate whether a treatment works or not? This is a causal question. One simple way is to conduct a Randomised Controlled Trial: we take a certain number of individuals meeting certain inclusion criteria, we toss a coin to decide which treatment they should receive and we compare the outcomes in the two groups which, on average, will differ only according to the treatment they received. Why can't we just give the drug to all patients, in the hope that it works, and see whether they get better? Without any evidence, not only we have no idea whether the drug will work, but it might even be harmful.
Now suppose the patients to whom we gave the drug feel better after few days. The reason why we need a control group (a group of patients being treated according to standard of care) is that, otherwise, we could not really know whether those patients would have healed anyway. Of course, ideally we would need to go back in time, give the dfferent treatment to the same patient, and compare the outcomes. This is not (yet) possible, so as this video explains, we instead randomise "otherwise similar" patients to either receive one treatment or the other. Why do we need randomisation? Can't we decide which patients to give one treatment or the other? Well, how would we make sure the patients were not chosen just to make one of the two treatments look better than the other? Having said all of these things, what would have been the best, simple, study that Raoult and friends could have used to investigate whether HCQ works? Yes, a Randomised Controlled Trial. Did they do it? Of course, not!
In their first study, few patients were assigned to receive either standard-of-care, HCQ alone, or in combination with another drug. No randomisation was used. How can we be convinced that the treatment actually worked? If you were interested, this article explains tons of other problems with this study, which I have no time to describe here. After this sudy, the Raoult group decided they would have not included further control groups in future research, on the ground of them not being ethical. Why so? Their rationale is that all patients, when ill, would rather have the doctors try a novel treatment on them, then do nothing. This is clearly a very flawed rationale. To explain why, let me use a simple example.
Imagine you were to jump from a plane, and they told you to choose between two parachutes: the first is a quite old model, on which we know quite a lot. It opens 95% of the time with no problem. There is also a novel model, on which we have no information at all. It is equally likely to open 100% of the times, and surely save your life, or to just never work. Which one would you choose? A randomised controlled trial, is basically an experiment in which somebody chooses which parachute to give you tossing a coin. Head the first, cross the second. Raoult point would basically be that this is not ethical, because giving somebody the old model is dangerous, because we know it kills 5% of people. I agree that doing a randomised control trial like this would be unethical, but for the opposite reason: I would NEVER trade a 95% effective parachute with one I know nothing about.
Now, suppose there were 30 people on a plane that only carries the new parachute type. The plane has a mechanical failure, so passengers have to use the 30 available parachutes. Only one passenger sadly fails to open their parachute. One in 30 is better than 1 in 20, so is the new parachute better? Who knows, we'd need to see whether the same people would have survived with the old parachute. But now, at least we have some info on the effectiveness of the new parachutes. A statistician might say that, from current information, the new parachute is between 85% and 100% effective. After this "trial", the previous experiment does not feel that unsafe anymore. Now, I'd be happy to be randomised to receive either of the two parachutes. I'd still think it is crazy to give the new parachute to everyone, just because of the very little experience of what happened on that plane.
The phases of clinical research work this way exactly to make sequential trials ethical. Phase 0, we throw a bunch of robots or rats wearing the new parachute. If a good portion of them survived, we proceed to Phase 1, where we ask volunteers to dive with the new parachute, giving them a reserve one, just in case. If the new parachutes appear safe after Phase 1, we proceed to Phase 2, in emergency settings. We compare two small groups of people that are randomised to receive either a new or old parachute. Finally, in Phase 3 we randomise a larger number of people. We only reach Phase 3 if the new parachute is at least decently safe and effective and it only stops being ethical randomising to the old parachute when there is overwhelming evidence that the new one is better.
Of course, if the risk of dying was much larger, we could think in a different way. If the old parachute was 5% effective, then I'd definitely prefer to try the new model, no matter what. In that case, though, a good idea would be to prepare two new models and compare at least one against the other.
The HCQ studies have gathered a lot of attention in media thanks to some (in)famous tweets from Trump, presenting HCQ as a game-changer. This has led to shortages of HCQ for people that needed it for conditions for which it has been proven to be effective. Now a new study under review suggests the complete opposite, so that HCQ may indeed to harmful. Again, the study is not an RCT though. In these situations, researchers should not conclude that either HCQ definitely does or does not work. Nobody knows. What a researcher concludes is "we need evidence". How can we obtain that evidence? Running well designed clinical trials.
I have my, possibly controversial, view on reporting clinical trials results in generalist media: only phase 3 trials should be reported. No early-phase study should be reported. Why? Because the average reader of a generalist journal cannot understand all these nuances, and will be given continuously false hopes. Newspapers should focus on results of large, phase-3, randomised controlled trials, similarly to how I think they should only report the results of causally-valid analyses. Early-phase trials, and correlation studies, should be left to discussion between experts.
There is one last question that friends and family keep asking me: will we find a vaccine first, or a treatment? I am not a doctor, nor Nostradamus, so it is impossible for me (and indeed for anybody else) to answer this question with certainty. There are however some points to consider: a vaccine will necessarily be a new drug, so it will have to go through all the phases (0,1,2,3). This will take time. Furthermore, I am not familiar with vaccine trials, but I imagine it will take some time to measure the outcomes, as patients will probably need to be followed for some time to see whether they develop the infection. On the contrary, a lot of clinical trials are being ran using treatments that have been developed for other diseases, so that phase 0 and 1 can be skipped. Secondly, there are a lot of recruitable patients at the moment, and trials for these treatments will probably require no more than around 30 days follow up. From this it stems that it is more likely that some treatment will be developed first, as it happened with SARS for example. However, I think it is important, for the casual reader with no experience of medical research, to know that the vast majority of treatments discovered are no panacea for all problems. Usually effects are moderate, and only a handful of treatments discovered in recent years had very strong effects. I can think of PrEP for HIV prevention, or immunotherapy against cancer. Most other treatments, often have little effects, which surely can help, but will likely not eradicate the disease. Again, I am no oracle: anything could happen, a vaccine could be developed soon, or never developed. An effective treatment could be the mother of all treatments, or no drug may be found helpful in two years time. But I am just talking about expectations, and what is the most likely course of drug development, given past experience in other diseases.

This pretty much sums up everything that I wanted to say about the current situation. I mainly talked about numbers, and interpretation of such numbers, here, because it is what I am more experienced with. Talking about numbers, though, often hides what lies behind these numbers. For me, a tragic reminder of this, was the loss of Harvey Goldstein a couple of weeks ago. Harvey was one of the most prominent statisticians in the UK (and in the world), particularly in the fields of multilevel analysis and educational statistics. See this obituary to read more about him. I had the luck to work with him since the beginning of my Ph.D, and indeed getting my Ph.D would have not been possible without his help. He was always kind and helpful with young researchers. A couple of days after the Italian outbreak exploded, he was the first person asking me if my parents were fine, where they were living, if they were staying safe, etc etc. Just over a month later, it was incredibly sad to hear that the "bastard" had brought him away. This post is, humbly, dedicated to him. To thank him for what he taught me (us) over the years.




Comments